近日，国际应用数学期刊Foundations of Computational Mathematics在线发表了北京大学数学科学学院胡俊教授课题组的论文 “ A construction ofconforming finite element spaces in any dimension ”，该文章讨论了任意维空间中单纯形网格上具有任意光滑性的有限元空间的构造，解决了有限元领域一个长期公开的难题。论文作者为胡俊教授、北京大学数学科学学院博士研究生林挺和吴清玉。

有限元方法诞生于上个世纪五、六十年代，最初主要用于弹性结构的应力分析，目前已经发展成为科学与工程计算中最主要的离散方法之一。有限元方法的基础是变分原理和分片多项式逼近，逼近连续问题相应泛函空间的离散空间为具有一定连续性的分片多项式空间，称为有限元空间。每个问题对有限元空间的连续性有各自的要求。二阶泊松方程的协调有限元方法要求其有限元空间具有连续性，双调和方程的协调有限元方法要求相应有限元空间具有连续性，以此类推阶椭圆边值问题的协调有限元方法要求其有限元空间具有连续性。

对于有限元，一个简单却应用非常广泛的例子是单纯形网格上的拉格朗日单元。对于二维情形，协调线性元的有限元空间是由如下所示节点上的帽子函数（hat function）张成的。

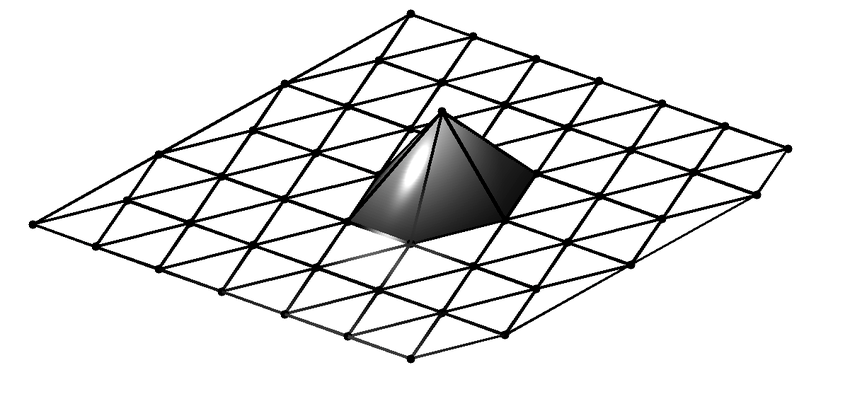
图片来源于网络

对于有限元，其构造远比有限元要复杂，所需的多项式次数高，自由度多，而且自由度涉及到高阶偏导数。对于二维一般的三角形网格，最低阶协调有限元由有限元方法奠基者之一的John H. Argyris于1968年提出，该单元使用了次数为5的多项式空间为形函数空间，每个三角形上有21个自由度，为三个顶点上有限元函数的函数值、一阶偏导数、二阶偏导数，和三条边中点的一阶法向导数值。而三维一般四面体网格上有限元的构造比二维情形复杂得多，最低多项式次数为9，每个四面体上有220个自由度，涉及有限元函数在四个顶点上的函数值、一阶到四阶偏导数，在六条棱上的一阶法向导数和二阶法向导数，四个面上的函数值和一阶法向导数，和四面体内部的函数值。文献中普遍猜测，在维空间中单纯形网格上构造有限元需要次多项式, 而构造有限元需要次多项式。但是，文献中没有成功构造出四维及以上空间中(时)有限元。注意到不同维数空间中的有限元空间的连续性具有某种传递性，即在维空间中构造有限元时，需要借助维空间中的有限元，而后者又需要维空间中的有限元。这种传递性使得从统一视角在任意维空间系统地构造具有任意连续性的有限元成为可能。

胡俊教授课题组的这一工作在维空间中单纯形网格上成功构造出有限元 (对任意非负整数)，使用的形函数空间为文献中普遍猜测的形函数空间，即次数为的多项式空间。该构造基于论文中建立的单纯形上有限元自由度与多重指标集的一个一一对应关系，这一对应关系依赖于通过一个非负整数连续性向量建立的多重指标集的一个精细内蕴分解。该内蕴分解的组合性质使得有限元空间连续性之间的传递性得以充分考虑和利用。通过提出一个集合-整数对的序，利用数学归纳法，该论文证明了自由度关于形函数空间的唯一可解性，进而证明了相应的有限元空间的连续性。

北京大学数学科学学院李若教授指出，单元的精巧构造是有限元方法中最具艺术性的部分，胡俊等人的这项工作是这种艺术性的一个典范，其结果也完全可以称为是令人吃惊的，一般地，具有高阶全局光滑性有限元空间尽管可以推测是存在的，但很难想象居然可以通过显式构造而获得。

美国宾州州立大学许进超教授也给予这项研究高度认可，他提到自上个世纪五、六十年代有限元方法诞生以来，任意维空间中单纯形网格上具有任意阶连续性的协调有限元方法的存在性及其构造问题是该研究领域一直没有解决的重要数学理论问题。这里的主要挑战是形函数空间和相应自由度的选取。对于二维情形，计算数学家James H. Bramble 和 Milos Zlamal于1970年在三角形网格上构造了一族协调有限元；而对三维情形，样条学者 Mingjun Lai 和 Larry L Schumaker于2007年在四面体网格上构造了一族协调有限元。对于四维及以上情形，文献中一直没有解决该问题。胡俊教授和他的两位博士研究生林挺与吴清玉通过建立多重指标集合的一个分解，揭示了泡函数空间的一个内蕴结构，设计了一个数学归纳法，最终非常漂亮地解决了这个长期悬而未决的难题。他们的结果是有限元方法数学理论方面的一个重要突破，而且为非协调元方法、间断Galerkin方法和虚单元方法等数值方法的数值分析提供了数学工具。

人员介绍

胡俊，北京大学数学科学学院教授。主要从事非标准有限元方法，特别是弹性力学问题及相关问题的非标准有限元方法的构造、数值分析及自适应有限元方法等方面的研究。他（部分与合作者）彻底解决了弹性力学问题混合有限元方法的构造这个有50余年历史的公开问题，首次构造出线性化Einstein-Bianchi方程组保结构的稳定混合有限元方法。曾获教育部自然科学奖一等奖、国家杰出青年科学基金、冯康科学计算奖、中国数学会计算数学分会首届青年创新奖。现任期刊Adv. Appl.Math.Mech.执行主编、期刊Comput. Math. Appl.,Comput. Methods Appl. Math.，CSIAM Trans. Appl. Math.， J.Comput.Math.和《数学理论与应用》的编委，北京计算数学学会理事长，中国数学会常务理事，中国数学会计算数学分会常务理事，当选为中国科协第十次全国代表大会代表和北京市科协第十届委员。

林挺，北京大学数学科学学院2021级博士研究生，本科毕业于北京大学数学科学学院。与合作者在Journal of the European Mathematical Society上发表论文一篇。入选北京大学应用数学卓越研究生计划。曾获北京大学未名学士、BICMR研究生奖。2023年获得EASIAM（SIAM东亚分会）最佳论文奖一等奖。

吴清玉，北京大学数学科学学院2022级博士研究生，本科毕业于北京大学数学科学学院。入选2022级数学学科研究生拔尖计划、北京大学应用数学卓越研究生计划。曾获北京大学第十三届“学生五·四奖章”、北京大学学生年度人物·2021、北京市优秀毕业生、北京市优秀学生干部、北大数学怀新学士等多项荣誉。

文章来源：北京大学数学科学学院

转载本网文章请注明出处