近日，北京大学数学科学学院、大数据分析与应用技术国家工程实验室、统计科学中心助理教授/研究员张瑞勋团队在AI+Finance基础理论方面的系列工作在国际运筹学顶级期刊Operations Research和人工智能领域顶尖会议AAAI Conference on Artificial Intelligence发表。

论文“On Consistency of Signature Using Lasso”发表在Operations Research，该研究证明了基于Lasso回归的Signature方法的统计相合性及收敛速度，实验表明Signature方法可被有效应用于机器学习中的特征提取，高精度地学习时间序列的非线性函数和期权等金融衍生品的价格，其性能取决于底层随机过程的特性以及Signature的选择。论文合作者为Xin Guo（加州大学伯克利分校教授）、王彬楠（北京大学数学科学学院博士生）和赵朝熠（麻省理工学院斯隆管理学院及金融工程实验室博士后，论文完成时为北京大学数学科学学院博士生）。

Signature在机器学习中是一种重要的特征提取与模式识别工具，其在医疗预测、交通运输、金融建模等领域展现出领先性能。Signature的数学定义为连续或离散时间随机过程的迭代路径积分，其Universal Nonlinearity性质能够将复杂时序数据的特征选择问题转化为线性建模问题，高效提取时序数据中的关键信息。尽管现有文献对Signature方法的概率性质研究日益丰富，但关于其统计性质的研究仍然较少。Signature可以在Itô积分或Stratonovich积分意义下定义，但二者的统计性质差异尚未厘清，现有研究通常任意选择其中一种定义来进行统计数据分析。

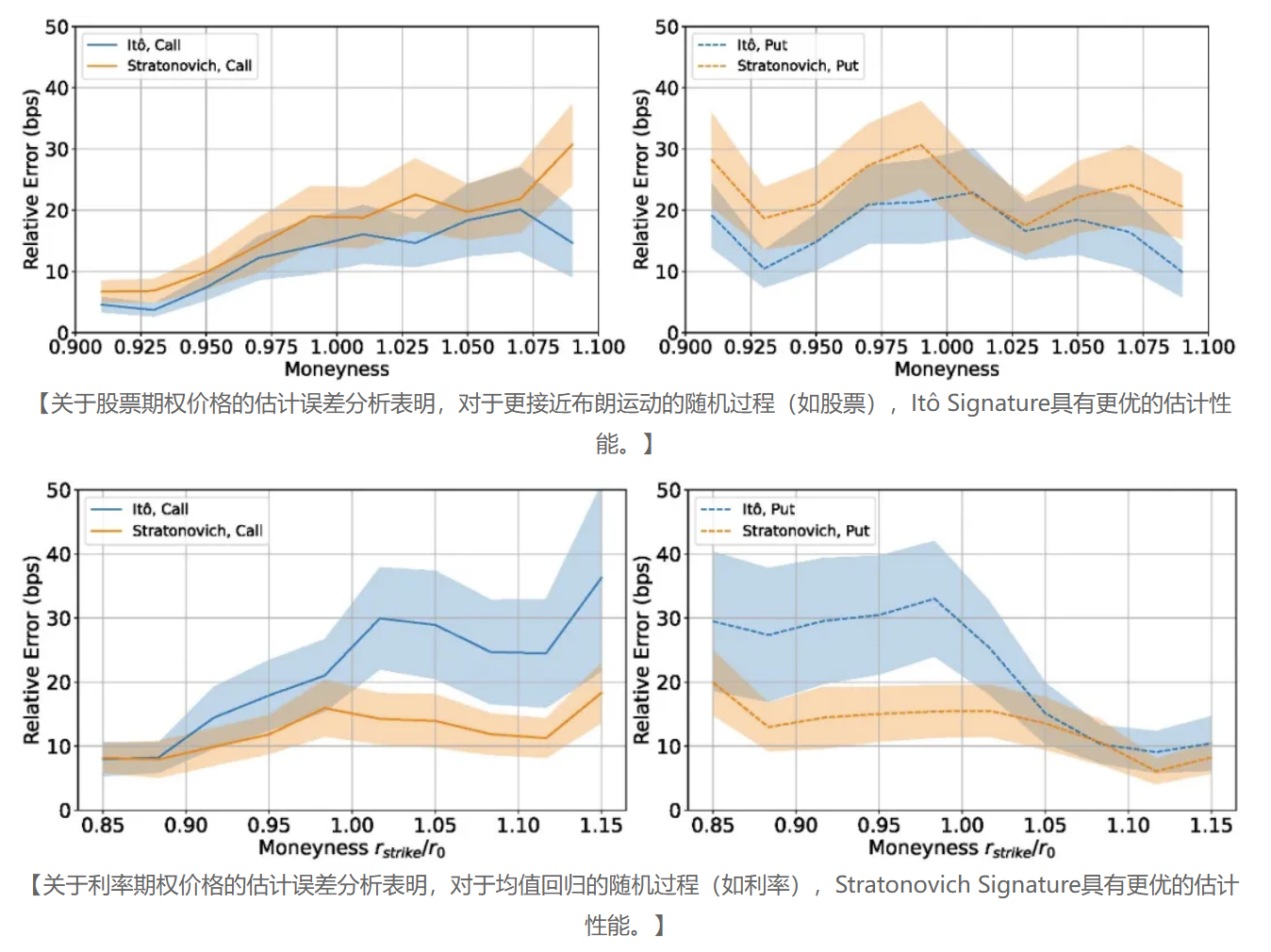
针对这一问题，该研究关注以Signature为自变量的Lasso回归的特征选择统计相合性。该性质是实现模型可解释性与样本外预测性的基础，为不同Signature定义的选择提供理论依据。研究分别证明了基于Signature的Lasso估计量在总体和有限样本下的相合性。数值实验进一步表明：对于更接近布朗运动且维度间相关性较弱的时序过程，采用Itô Signature的Lasso回归具有更强相合性；对于均值回归特性更强的过程，Stratonovich Signature表现更优。在应用层面，研究表明Signature方法能以高精度学习非线性函数，并可通过学习Arrow–Debreu状态价格来对股票期权与利率期权进行定价，这种方法具有可解释性，且可进一步迁移至其他金融衍生品的定价之上。

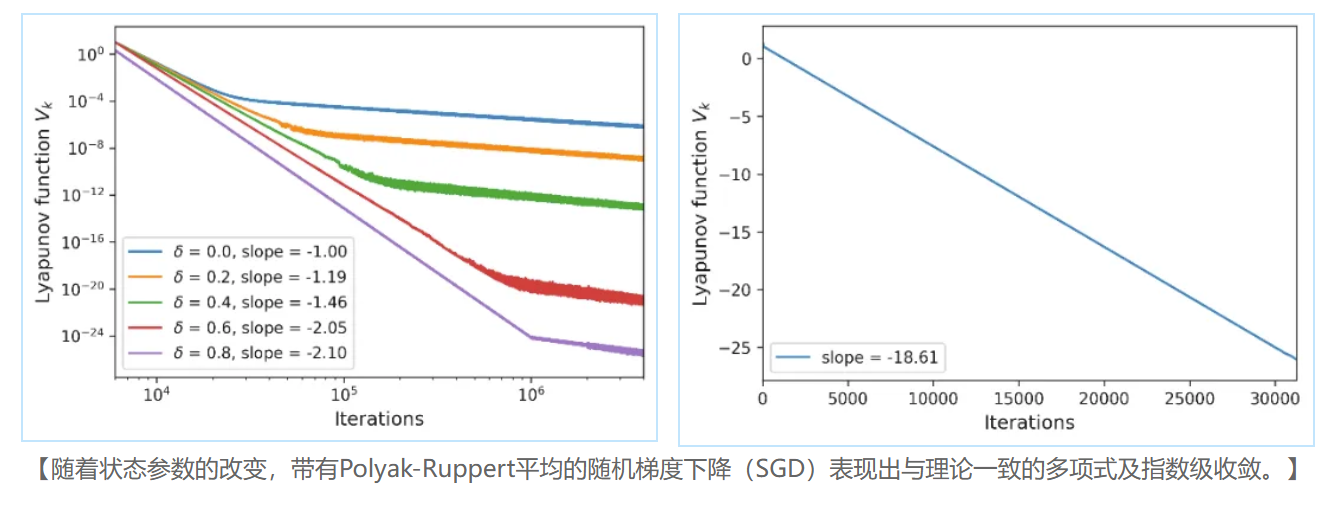
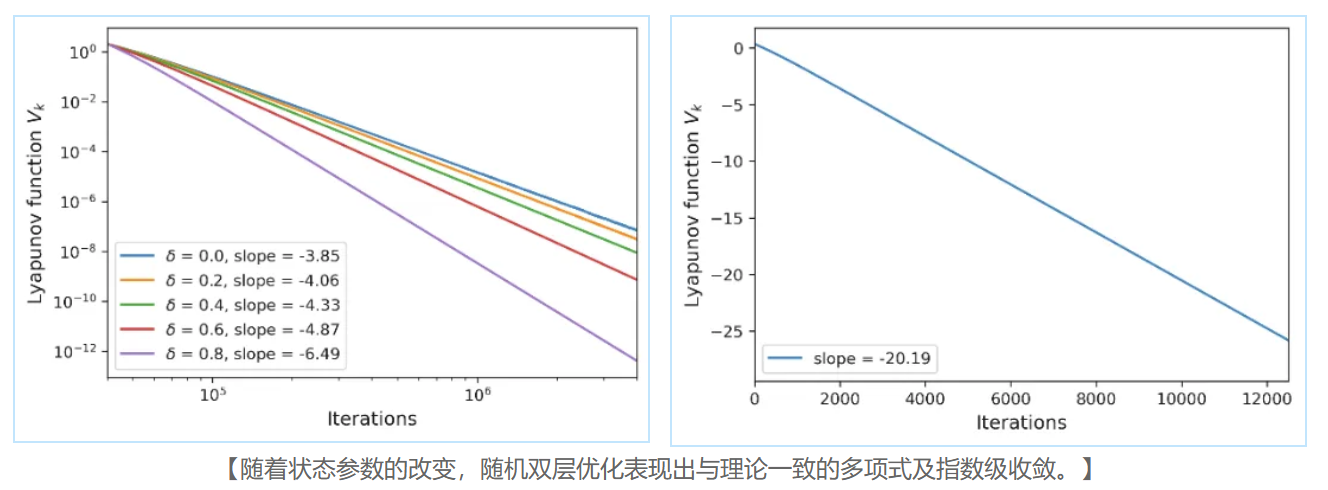
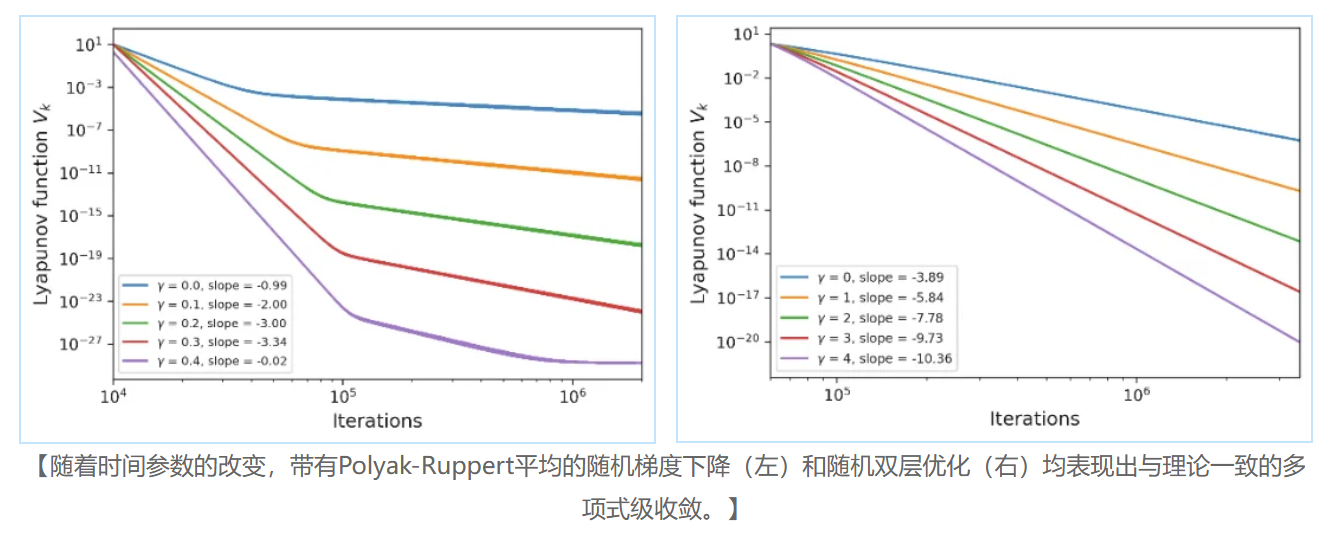
论文“Convergence Rate in Nonlinear Two-Time-Scale Stochastic Approximation with State (Time)-Dependence”发表在AAAI Conference on Artificial Intelligence，该研究考虑双时间尺度随机逼近（Two-time-scale stochastic approximation）中状态相关和时间相关的噪声情形，证明了在这两种情况下Lyapunov函数均表现出多项式收敛速率，且其速率与状态或时间相关噪声的参数密切相关。研究通过两个数值实验验证理论结果，包括带有Polyak-Ruppert平均的随机梯度下降和随机双层优化。论文合作者为陈梓西（北京大学数学科学学院本科生）和徐昱旻（北京大学数学科学学院博士生）。

随机逼近（Stochastic approximation）广泛应用于机器学习、强化学习与随机优化等领域，它是一类经典的迭代方法，用于在无法精确观测函数值、仅能获得带噪反馈的情况下寻找最优解。为适应复杂系统中不同变量演化速度差异的情形，研究者进一步发展出“双时间尺度随机逼近”（Two-time-scale stochastic approximation）方法，引入两个不同比例的步长来同时更新快变量与慢变量，从而更有效地刻画它们的交互关系。尽管该方法具有重要应用潜力，现有理论仍面临若干关键挑战：大多数结果依赖于理想化的噪声假设、变量耦合使得收敛分析更为复杂、以及在高噪声或非平稳环境下收敛速度仍显不足。

该研究提出一种新的参数化框架，以突破双时间尺度随机逼近在高噪声或非平稳环境下收敛速度受限的瓶颈。通过引入随状态和时间衰减的参数，有效控制关键噪声项的方差，提升算法的收敛性能。结果表明，在合理设定下，误差衰减可达任意多项式甚至指数级，优于现有理论。数值实验进一步验证了本文提出的方法在不同类型噪声下的收敛性能，展示了理论分析的有效性与广泛适用性。该结果为构建收敛更快、稳健性更强的优化算法提供启示，为强化学习、高维随机优化及其他高噪声复杂系统中的实际应用奠定理论基础。

张瑞勋

北京大学数学科学学院助理教授/研究员、金融数学系副主任，大数据分析与应用技术国家工程实验室、统计科学中心助理教授/研究员。入选国家海外高层次人才计划青年项目。北京大学数学与应用数学、经济学（双学位）学士，麻省理工学院（MIT）应用数学博士。主要研究领域包括机器学习方法与金融的交叉、市场微观结构、绿色金融、适应性市场理论。主持国家重点研发计划青年科学家项目、国家自然科学基金面上项目等，研究工作发表在PNAS、Management Science、Operations Research、SIAM Journal on Financial Mathematics, AAAI等国际期刊和会议上，获标普全球ESG学术研究奖、ICPM学术研究奖、Questrom–CEMA最佳论文、CFRI&CIRF最佳论文、北京大学黄廷方/信和青年杰出学者等奖项。

Operations Research是美国运筹学与管理科学研究协会（INFORMS）出版的旗舰期刊，创办于1952年，是运筹和金融工程领域国际公认的顶尖学术期刊。The AAAI Conference on Artificial Intelligence（AAAI）会议是由美国人工智能协会（AAAI）主办的国际人工智能领域旗舰会议，创办于1980年，是人工智能领域国际公认的顶尖学术会议之一。论文作者均按姓氏首字母序，张瑞勋为两篇文章的通讯作者，研究受到国家重点研发计划（2022YFA1007900）、国家自然科学基金（72342004, 12271013）、银华教育基金会等项目资助。

【参考文献】

[1] Xin Guo, Binnan Wang, Ruixun Zhang, and Chaoyi Zhao (2025). On consistency of signature using Lasso. Operations Research, article in advance.

[2] Chen, Z., Xu, Y., & Zhang, R. (2025). Convergence Rate in a Nonlinear Two-Time-Scale Stochastic Approximation with State (Time)-Dependence. Proceedings of the AAAI Conference on Artificial Intelligence, 39(15), 15993-16000.

【链接】

在线论文：https://doi.org/10.1287/opre.2024.1133

在线论文：https://doi.org/10.1609/aaai.v39i15.33756

转载本网文章请注明出处