本文从数据的角度简单介绍了人工智能的各种不同方法，重点强调小数据方法和大数据方法在处理复杂任务以及相应的组合爆炸和维数灾难问题能力上的本质区别。最后，简单讨论如何寻找适合中国国情的人工智能发展道路。

人工智能的零数据、小数据、大数据和全数据方法

作者：鄂维南院士

2024年6月召开的中国科学院院士大会上，我应邀作了一个以“数学与人工智能”为题的大会报告。会后许多院士都希望我把报告的主要内容写出来，这是这篇短文的由来。在这篇文章中，我试图用相对通俗但又不掩盖核心问题的语言解释人工智能的一些主要方法和它们各自的特点。

人工智能的众多不同方法，可以根据其所用数据量的大小，分为零数据、小数据、大数据和全数据方法。当然，数据不是人工智能发展的唯一线索，但它可以比较方便地帮助我们梳理人工智能发展过程中出现的不同想法。

01零数据

逻辑推理、符号计算、专家系统等原则上都不需要数据。逻辑推理方法的主要思路是构造算法和软件模仿人的推理过程。符号表示和符号计算试图把逻辑推理更加形式化、自动化。在1956年的达特茅斯(Dartmouth)会议上，纽厄尔(Newell)、肖(Shaw)和西蒙(Simon)推出的逻辑理论(Logic Theorist)系统就是一个这样的例子。逻辑理论被认为是第一个人工智能系统，它能够证明许多数学定理，还能下棋。

专家系统的目标是把专家知识用软件系统实现运用。专家系统最成功的例子是IBM的深蓝(Deep Blue)，它在1997年战胜了国际象棋冠军卡斯帕罗夫(Kasparov)。其他零数据方法方面典型的工作包括LISP语言和数学定理机器证明的“吴方法”。

02小数据

线性回归、逻辑回归、支持向量机等统计学习方法是典型的小数据方法。早期的神经网络，如感知机(perceptron)，也是小数据方法。隐式马尔可夫过程(HMM)、N-gram、深度学习出现之前的机器学习方法等，也都是小数据方法。过去的模式识别、自然语言处理、语音技术、机器人技术等都是基于小数据（或零数据）方法实现的。很长一段时间里，人工智能是靠这类方法支撑的。

零数据和小数据方法往往对简单问题（如跳棋、象棋等）比较有效，但是在复杂问题面前无能为力。具体地说，它难以克服“组合爆炸”和“维数灾难”引起的困难。组合爆炸是指当系统变大的时候，所有可能出现的组合爆炸性增加。例如从国际象棋到围棋（见图1），棋盘从8×8变成19×19，其所有可能的组合增加了多个数量级。零数据方法虽然能够解决国际象棋问题，却难以解决围棋问题。

图1 国际象棋（左）与围棋（右）棋盘（图来自互联网）

维数灾难是指当一个问题的自由度（即维数）增加的时候，计算复杂性呈指数增加。小数据方法可以处理低维问题，但是难以处理高维问题。对于图像识别、量子化学、动态规划和非线性统计等领域的高维问题，人们只能通过经验、特征工程或者极端的简化方法处理。量子化学中的哈特里(Hartree)或者哈特里-福克(Hartree-Fock)方法，以及非线性统计中的广义线性模型(generalized linear models)等都是极端简化方法的例子。

人工智能经过了几次大起大落，本质上都是由于对组合爆炸和维数灾难的困难程度认识不足引发的。最近几年，我国仍有团队提出摆脱大数据、以小数据方法实现通用人工智能。这个方案的核心问题是它能否克服组合爆炸和维数灾难引起的困难。如果这种思路能够有效解决围棋问题，那么它和传统的零数据、小数据方法必然有着本质的不同。如果不能，那么基于这种思路建立的通用人工智能系统最多也只是一个“弱智”系统。这并不是说零数据、小数据方法在处理复杂问题时没有用，而是说仅仅靠这些方法难以走得很远。我们必须对此有正确的认识。

03大数据

尽管深度学习受到热捧之前人们就已经在处理和分析大数据，但是真正让大数据充分发挥作用的方法是深度学习，其标志性事件是辛顿(Hinton)团队于2012年赢得ImageNet图像识别比赛冠军。辛顿等人设计并训练了一个神经网络，取名AlexNet。AlexNet有5层卷积网络、3层全连接网络，6000多万个参数。相比较而言，之前杨立昆(Yann LeCun)训练的Le-Net只有几万个可训练参数。

需要强调的是，辛顿等人在训练AlexNet的时候用的主要算法，如随机梯度下降、反向传播等都是已知的。辛顿团队的工作就是充分训练了这样一个多层神经网络。要做到这一点，就需要高质量的数据资源和一定的算力资源。这正是ImageNet和GPU发挥作用的时候。所以辛顿等人的工作既是技术上的成功，更是信念上的坚持带来的成果。辛顿等人的工作不仅改变了图像识别，而且改变了整个人工智能领域，因为基于神经网络的深度学习方法是一个通用方法。神经网络其实就是一类函数，它与多项式这类函数的不同之处在于它似乎是逼近多变量函数的有效工具。也就是说，它能够有效地帮助我们克服维数灾难和组合爆炸引起的困难。事实上，基于深度强化学习的人工智能方法，AlphaGo很快就在围棋比赛中战胜了人类最好的选手。神经网络也被用来解决科学领域碰到的多个自由度的问题，如蛋白结构问题、分子动力学势能函数问题等，并由此催生出一个崭新的科研范式：AI for Science。正因为深度学习在多变量函数逼近这样一个非常基础性的问题上带来了巨大突破，所以它在各种各样的问题上都给我们带来了新的可能。需要强调的是，尽管很多成功案例都表明深度学习方法是解决高维问题的一个有效工具，但我们对其背后的原因了解得还很不充分。从数学的角度来说，这是一个非常优雅、非常清晰的数学问题，它将推动高维分析的发展。关于这方面的工作，请参见我在2022年国际数学家大会上的报告。早在20世纪40年代，麦卡洛克(McCulloch)和皮茨（Pitts）就提出了神经网络的概念。50年代，罗森布拉特（Rosenblatt）又提出了感知机的概念。为什么要一直等到2010年左右，人们才开始真正认识到神经网络的巨大威力？我认为其根本原因有两个：一是训练好神经网络需要一定的高质量数据和算力资源，这些条件是一个门槛；二是人们缺乏对神经网络的正确认识。明斯基(Minsky)和佩珀特(Papert)合著了一本很著名的书，就叫“感知机”(Perceptron)。这本书研究的一个主要问题是：什么样的逻辑函数可以用（两层）感知机精确表示出来？结果他们发现，一些简单的逻辑函数都无法用感知机精确表示。这本书的出版给整个神经网络领域的发展带来了巨大负面影响。究其原因，明斯基和佩珀特的出发点是错误的：我们应该把神经网络看成是逼近函数的工具，而不只是看它能够精确表达什么函数。而从函数逼近的角度来说，神经网络不仅能够逼近一般函数(universal approximation theorem)，而且基于神经网络的逼近和基于其他传统方法的逼近有着本质区别：传统逼近方法有维数灾难问题，而神经网络在高维或者多个变量的情形下仍然很有效。当然，除了维数灾难和组合爆炸之外，还有许多其他问题需要考虑。比如，对文本这类时间序列数据来说，能否处理长期记忆(long-term memory)是一个重要问题。有结果表明，循环神经网络(RNN)有记忆灾难问题：即当记忆长度增加时，所需要的神经元个数呈指数增加。而transformer网络没有这个问题。事实上，有理论结果表明，transformer网络的确能够有效表达长程但稀疏的记忆依赖关系。这正是大语言模型所需要的。

04全数据

大数据方法考虑的是单个数据集，全数据方法的思路是把所有数据都用起来。比方说，把互联网上所有高质量文本数据都用起来。这里有两个关键问题，一是绝大部分数据都是无标注数据，如何用好这些无标注数据？预训练方法就是为了解决这个问题而诞生的。二是既然我们把所有数据都用了，就得把所有可能的下游问题都解决了。也就是说，我们的目标必须是某种形式的通用人工智能系统。这就催生了有监督的微调（SFT）技术。目前这个思路最成功的实践出现在文本领域。对文本来说，有两个最典型的预训练框架。一是谷歌的BERT，它的出发点是填空；二是OpenAI的GPT，它的技术路线是预测下一个词。就目前的发展情况来看，GPT占了绝对优势。究其原因，是BERT试图靠上下文内容进行语义理解（双向预测），而GPT只根据过去预测未来（单向预测），所以GPT既是一个生成模型，又是文本任务的一个通用模型：只要能够预测下一个词，我们就可以解决文本领域的所有问题，包括翻译、对话、写作等。从智能的角度来说，如果一个机器能够在不同场景下把预测下一个词的任务做好，那么它的文本能力就不低于人类。也就是说，它具备了一定的智能的本质特性。相比较而言，BERT完成的是一个更加简单的任务，因为它能够利用后面的文本内容帮助完成填空问题，所以它不需要很强的智能能力。从理论上来看，大模型带来的最突出的现象是缩放定律(scaling law)和相应的涌现现象(emergent behavior)。缩放定律源于复杂系统研究，是指当系统规模变大时，相关指标会按照一定的规律变化。在大模型领域，它有两方面的意义。一方面，它让我们可以从训练小一点的模型出发，估算出训练大模型所需要的计算量和数据资源；另一方面，它为提升模型的功能提供了一个指导方向。从后者的角度来看，缩放定律起的作用有点像摩尔定律。

应该强调的是，缩放定律和涌现都是在复杂系统中经常能看到的现象。不同的技术框架可以有不同的缩放定律，而优化缩放定律应该是我们追求的主要目标之一。当然，我们也可以问：就像摩尔定律一样，缩放定律终究会有停滞的时候，下一步该如何发展？我们还可以把这些不同方法组合在一起，构建更加有效的方法。一个例子是DeepMind推出的AlphaGeometry，它求解国际奥林匹克数学竞赛中平面几何题目的能力接近了人类最高水平（见图2）。它的主要想法是把逻辑推理方法和经验方法相结合：定理库和树搜索提供具体证明，而机器学习模型提供思路，比如如何加辅助线。毫无疑问，这类想法有着巨大的发展空间。

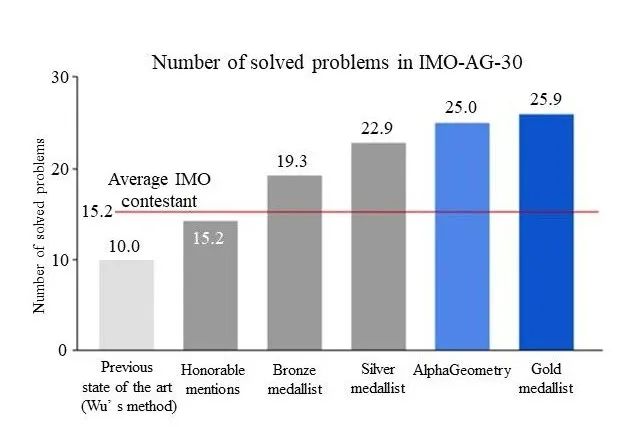
图2 AlphaGeometry将目前模型的几何定理证明水平从低于人类水平提高到接近金牌水平

从长远的角度来看，目前以GPT为代表的技术路径并不适合我国的国情。首先，在相当长的一段时间里，我国的算力与美国的相比将会有相当大的差距。目前国内大模型第一梯队的算力资源基本上是万卡规模（比如英伟达A100），而美国第一梯队是10万卡甚至更大规模。这就意味着在不远的未来，许多致力于开发基座模型的团队可能不得不停下追赶的脚步。其次，GPT存在许多浪费。我们应该寻找更加低能耗、低成本的替代路径。最近推出的“忆立方”（Memory3）模型就是一种这样的尝试。它用内置数据库的办法处理（显性）知识，避免把知识都存放到模型参数中，这样可以大大降低对模型规模的要求。最后，GPT并不能解决所有问题。在许多方面，比如图像，我们还需要寻求更加有效的技术方案。什么才是适合我国国情的人工智能发展路径？如何才能保证我国的人工智能长期稳定地发展？要回答这些问题，我们必须在以下两方面尽快布局。一是建立起一个完整的人工智能底层创新团队和创新体系，在模型架构、AI系统、数据处理工具、高效训练芯片等方向追求新突破；二是探索人工智能的基本原理，尽管我们与掌握人工智能的基本原理还有很大差距，但是我们已经具备了探索这些基本原理的条件。而长期稳定发展的技术路线，必然会在这个探索过程中产生出来。

致谢：在这篇文章的写作和院士大会报告的准备过程中，我得到了黄铁军、杨泓康、袁坤、朱松纯等老师的帮助。在此一并表示感谢！

作者简介

鄂维南

中国科学院院士，美国数学学会会士，美国工业与应用数学学会会士，英国物理学会会士。北京大学讲席教授、大数据分析与应用技术国家工程实验室主任、北京大学国际机器学习研究中心主任、北京科学智能研究院院长、北京大数据研究院院长、CCF会士。1982年毕业于中国科学技术大学数学系，1985 年获中国科学院计算中心硕士学位，1989 年获美国加州大学洛杉矶分校博士学位。主要从事计算数学、应用数学及其在力学、物理、化学和工程等领域中的应用等方面的研究。曾获首届美国青年科学家及工程师总统奖，冯康科学计算奖，国际工业与应用数学协会颁发的Collatz 奖，ICIAM麦克斯韦奖，美国工业与应用数学学会R.E.Kleinman奖，美国工业与应用数学学会卡门(Theodore von Karman)奖，SIAM和ETH Zürich联合授予的Peter Henrici奖及ACM戈登·贝尔奖（ACM Gordon Bell Prize），第五届北京市华人华侨“京华奖”。2022 年国际数学家大会1小时报告人。

转载本网文章请注明出处